Game 4 looks as follows:
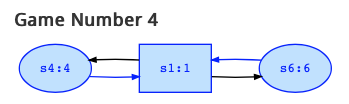
The highest rank is h=6, so that player 0 can win if player 0 can mange to visit the states with that rank infinitely often. Player 0 controls the oval nodes, and player 1 controls the rectangles nodes. Attractor(0,{s6}) are those states where player 0 can enforce that state s6 is reached whatever player 1 might try to avoid this. So, in state s6, we are already there, so that clearly, we see that in general Q is a subset of attractor(i,Q). State s1 does not belong to the attractor, since player 1 controls that state and player 1 might choose the transition to state s4 instead of the one to s6. The game may continue alternating between s1 and s4, so that s6 is never reached. For the same reason, also s4 is not part of the attractor, so that attractor(0,{s6})={s6} holds.
Note that player 0 still wins in all of the states of that game, since player 0 may choose the transitions in blue in the oval nodes. If player 1 infinitely often chooses the transition to s6, the highest rank visited infinitely often is 6 so player 0 wins, and otherwise, the highest rank visited infinitely often is 4 so player 0 wins also.
Game 3 looks as follows:
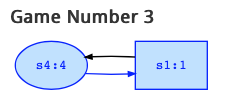
The highest rank is h=4, owned by player 0, and it only is the rank of state s4. We have attractor(0,{s4}) = {s1,s4} since it is clear that s4 belongs to the attractor. Also s1 belongs to the attractor since player 1 can only choose the transition to state s4, so that player 1 cannot avoid that s4 is reached.
So, in general attractor(j,Q) is the set of states where player j can enforce that a state in Q is reached, no matter what transitions the other player chooses in the states controlled by that other player. This can be expressed formally in µ-calculus as µx.(Q | <j>x) where ⟨A⟩φ := A ∧ ♦φ ∨ B ∧ φ = (A ⇒ ♦φ| φ), but in most cases, it can be seen from the game which states belong to the attractor.