You have to consider the automaton and have to determine the sequences that are accepted by the automaton.
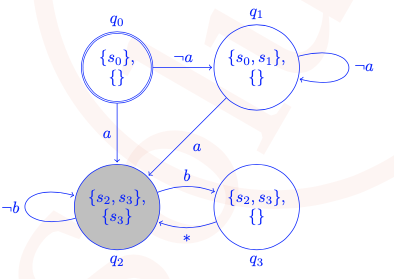
It is a deterministic FG automaton where we finally have to repeat the self loop on q2. Hence, we start in the initial state q0 and wait there for an occurrence of "a": As long as !a holds, we wait for "a" in q1, and if "a" is there, we switch to q2. After the first point of time where "a" holds, we switch between states q2 and q3 where only b matters. To satisfy the acceptance condition, we finally have to remain in state q2.
This can be expressed in different ways in LTL. For instance, we could write [(F G !b) SW a] or alternatively (F a) & (F G !b).
So, there is no general formula that you can apply here, but you need to understand what the automaton wants and you then have to describe that in LTL (in your words/symbols).
Having written this, I should also add that for non counting automata (but not for others), there are also algorithms that can translation the noncounting automaton to an LTL formula, but that is beyond the scope of the lecture.