In general, the existential successors of a state set φQ under a transition relation φR are computed as new2old(∃x1....∃xn.(φR∧φQ) where the function new2old replaces all variables x' to encode the target states by their corresponding variable x used to encode the current state.
To compute the set of states, the quantifiers in the above formula have to be eliminated which is done by their definition, i.e., ∃x.φ is replaced with φ[x<-0] ∨ φ[x<-1] (which is the disjunction of the cofactors by x). It is recommended to plan the right variable ordering in which the quantifiers are eliminated: While the result will be the same, the work may significantly differ. Moreover, the following rules are often useful and applied below without mentioning:
- x∧φ = x∧φ[x<-1]
- ¬x∧φ = ¬x∧φ[x<-0]
- x∨φ = x∨φ[x<-0]
- ¬x∨φ = ¬x∨φ[x<-1].
In the particular example, we have the following:
new2old(∃p.∃q.∃a.∃o.(next(p)<->¬(next(q)->(o ∨ q->(a<->p))))∧¬(a∧p))
= new2old(∃p.∃q.∃o.
(next(p)<->¬(next(q)->(o ∨ q->(0<->p))))∧¬(0∧p) ∨
(next(p)<->¬(next(q)->(o ∨ q->(1<->p))))∧¬(1∧p)
)
= new2old(∃p.∃q.∃o.
(next(p)<->¬(next(q)->(o ∨ q->¬p))) ∨
(next(p)<->¬(next(q)->¬(o ∨ q)))∧¬p
)
= new2old(∃q.∃o.
(next(p)<->¬(next(q)->(o ∨ q->¬0))) ∨
(next(p)<->¬(next(q)->¬(o ∨ q)))∧¬0 ∨
(next(p)<->¬(next(q)->(o ∨ q->¬1))) ∨
(next(p)<->¬(next(q)->¬(o ∨ q)))∧¬1
)
= new2old(∃q.∃o.
(next(p)<->¬(next(q)->1)) ∨
(next(p)<->¬(next(q)->¬(o ∨ q))) ∨
(next(p)<->¬(next(q)->¬(o ∨ q)))
)
= new2old(∃q.∃o.
(next(p)<->0) ∨
(next(p)<->¬(next(q)->¬(o ∨ q)))
)
= new2old(∃q.∃o.
¬next(p) ∨
(¬(next(q)->¬o∧¬q))
)
= new2old(∃q.
¬next(p) ∨
(¬(next(q)->¬0∧¬q)) ∨
(¬(next(q)->¬1∧¬q))
)
= new2old(∃q.
¬next(p) ∨
(¬(next(q)->¬q)) ∨
next(q)
)
= new2old(∃q.
¬next(p) ∨
(¬(0->¬q)) ∨
next(q)
)
= new2old(∃q. ¬next(p) ∨ next(q) )
= new2old( ¬next(p) ∨ next(q) )
= ¬p ∨ q
Apart from this, one may of course also use the BDD algorithms for quantifier elimination. In the above example, we obtain the following BDD for the conjunction of the transition relation and the state set (where next(p) and next(q) are written as p1 and q1, respectively):
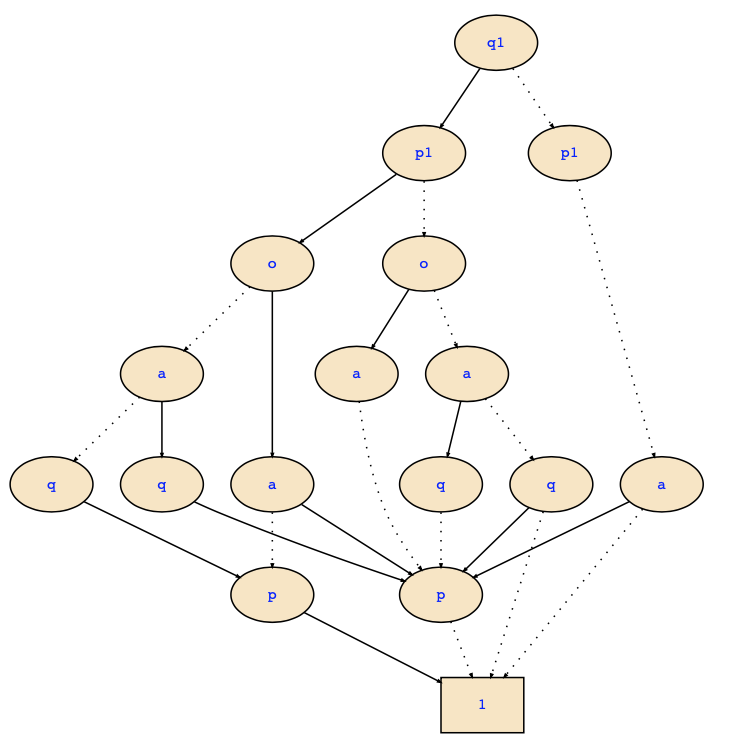
While it is a lot of work to construct this BDD, it is maybe interesting to point out that we don't need to have it in full detail, and therefore it would be enough to make a Shannon decomposition by q1 and p1. Since all variables are quantified out except for q1 and p1, all paths leaving nodes labeled with p1 lead to the 1-leaf. This will eliminate the leftmost node of p1 and will then give us the final result:
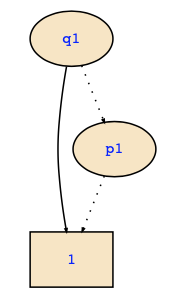
However, the use of BDD algorithms is not recommended for manual computations, in the computer, it would however usually be the most efficient way to solve the problem.