How to get set representation of ZDD for "Ф"

Question

I have given FDD with var order a < b < c. First question was to construct a propositional formula in RMNF. My solution was (b ^ c ^ a&c ^ b&c ^ a&b&c) and it is accepted by the exercise system. Second question is asking to find SET representation of ZDD for Ф. So, original SET that I found in task 1 from FDD is not accepted. Then I tried to get set for DNF and convert it to ZDD set. But it is also not accepted. Can anybody suggest, how can I get SET representation of ZDD?

My initial set, that I got for FDD was {{b}; {c}; {a, c}; {b, c}; {a, b, c}}.

Answer 1

If you computed the RMNF correctly, the FDD you have had must look as follows: 

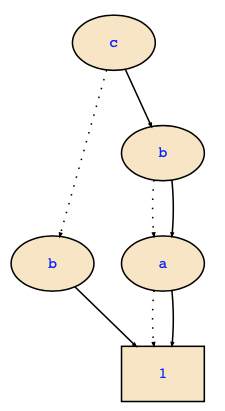
Its set representation is {{a,b,c},{a,c},{b,c},{b},{c}} as you said, and therefore the RMNF of this formula Ф is a∧b∧c ⊕ a∧c ⊕ b∧c ⊕ b ⊕ c.

To get the ZDD, you can convert this formula into its a disjunction of minterms (not just one of the DNFs, it must be THE disjunction of all minterms that satisfy the formula). If you compute the truth table, you get the following five minterms

• a∧b∧c
• a∧¬b∧c
• ¬a∧b∧c
• ¬a∧b∧¬c
• ¬a∧¬b∧c

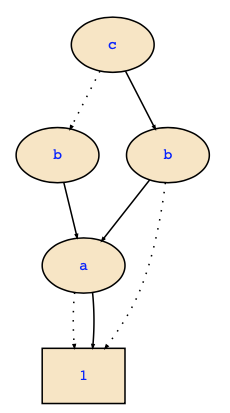
Their set representation is {{a,b,c},{a,c},{b,c},{b},{c}} (since we are supressing the negative literals) which corresponds with the following ZDD (it stores this set of sets of variables):

Note that formulas can have many DNSs, and even more than one minimal DNF. For example, DNFs of the above formula are the following ones:

• ¬a∧¬b∧c ∨ a∧b∧c ∨ a∧b∧¬c ∨ ¬a∧b∧c ∨ ¬a∧b∧¬c
• ¬a∧¬b∧c ∨ b∧c ∨ b∧¬c
• b ∨ ¬a∧c

Note again that for the ZDD, you need the disjunction of minterms (and minterms list all variables) which is canonical in contrast to most other DNFs (with exceptions like the Blake canonical form etc.).