You are confused because player 0 has a winning strategy in state s3 which is true as you can see with the result that the tool finally computes. However, for the first recursive call, we remove the attractor A := attractor(0,Qh) := {s1,s3,s5} so that these states do no longer belong to the game1 that is solved in the recursive call. Hence, these states will neither occur in win0' nor in win1'. For the first recursive call, we consider the following game:
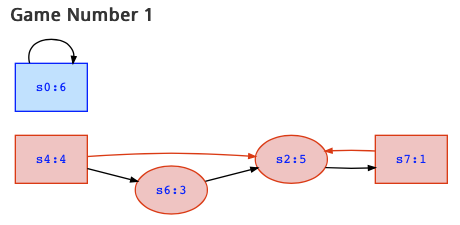
For your second question, look at the above game graph. Player 1 has a winning strategy in states s4 and s6, since in s4 player 1 can choose the transition to s2 (but even the other one will also do), and in s6, player 0 has no other choice than also moving to s2. In s2, player 0 has no other choice than moving to s7 where player 1 moves back to s2 which generates an infinite play where s2 and s7 occur infinitely often. Hence, the highest rank that appears infinitely often is 5 which is odd, so that player 1 win in the states s4 and s6 for sure.
Right?