CTL and CTL* satisfiability checking

Question

Exam Problem : 29.08.2017 : Q 8 e : 2017.08.29.vrs.solutions.pdf (uni-kl.de)

Problem :

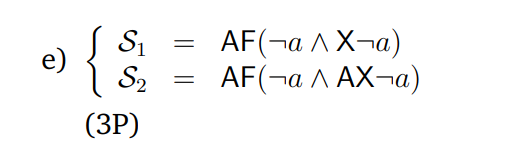
My Solution :

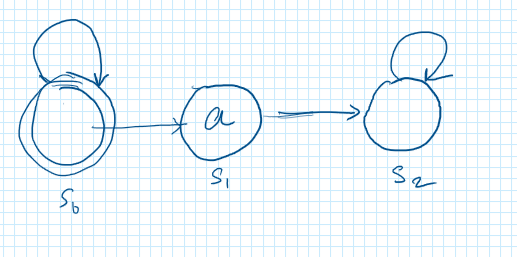
I thought it like below to satisfy S1 and not S2:

X !a holds in {s0, s1, s2}

!a holds in {s0, s2} 

!a & X !a holds in {s0, s2} 

AF (!a & X !a) holds in {s0, s2} 

Hence it satisfies S1.

X !a holds in {s0, s1, s2}

AX !a holds in {s1, s2}

!a & AX !a holds in {s2} 

AF (!a & AX !a) holds in {s1, s2} => (There is path in s0 in which it can loop forever and never reach s2)

No initial set, hence not satisfied.

Q1. Could you please let me know if my Kripke Structure is correct ?

Q2. Could you please let me know if my way of proofing is correct ?

Thanks in advance

Answer 1

Your Kripke structure and your arguments are fine, but your proof is now well presented. You should not say that a path formula like X!a holds in {s0, s1, s2} since path formulas hold on paths.

For S1, you should rather argument about the two paths s0^omega nd s0^*.s1.s2^omega leaving s0, both satisfy !a&X!a. For the other formula, which is a CTL formula, state-based reasing is appropriate.