Q: 13.02.2019 : Q 8 (e) : 2019.02.13.vrs.solutions.pdf (uni-kl.de)
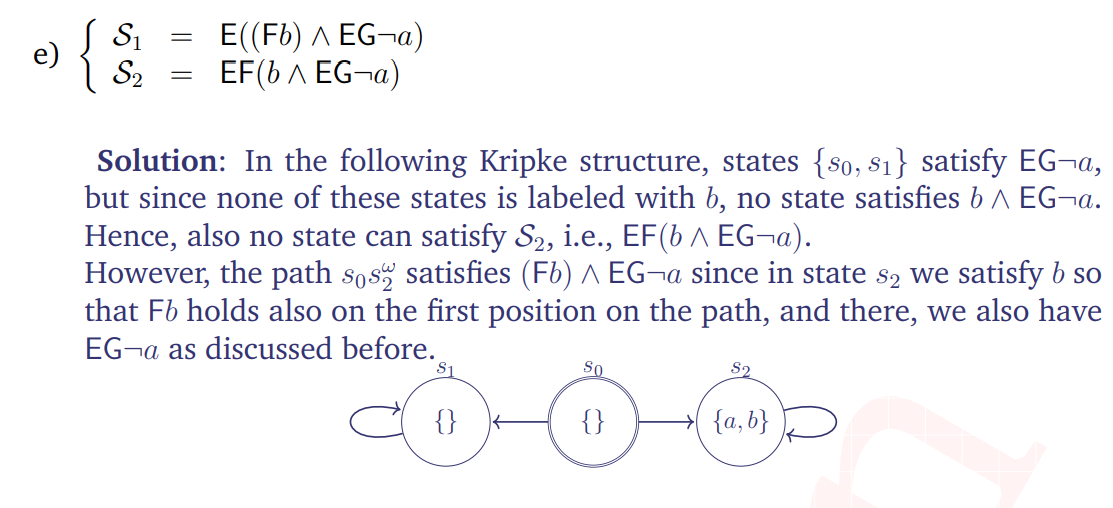
In this question I am having some trouble in figuring out the branching.
Like in S1 E ((Fb) & EG!a) :
-> The outer E says there exist a path on which Fb & EG!a holds. Suppose we have selected a path s0 -> s2, now :
Q Do I need to satisfy ((Fb) & EG!a) on that path only (s0 -> s2)? or it means choose any path from initial state only ?
Q And for the internal E how should I interpret this as a new branch on that path i.e from s2 or it refers to a branch from initial state only ?
Could you please explain how to intuitively think about these types of problems where paths are defined inside bracket as well ?
How to branch from where to branch ?