As far as I can see, the state transition diagram of the automaton is correct, the teaching tool gave me this picture which looks same:
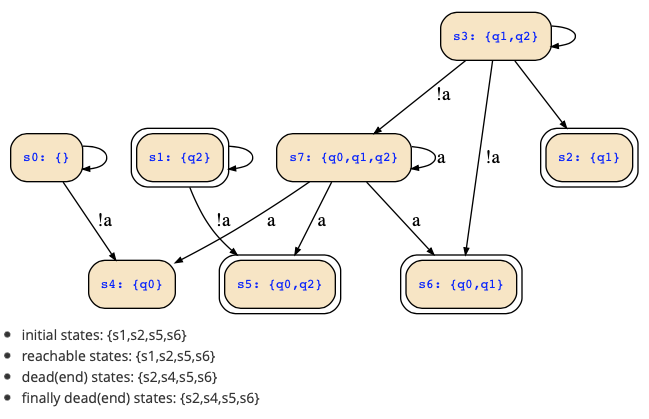
As we are only interested in infinite runs, we may exclude the finally dead states, and also the unreachable states, of course. What is left is just the self-loop in state s1 that can be taken with any input. That is the only infinite run of this automaton.
Let's check the acceptance conditions on that path:
- GF(a->q0) can hold (if we always use input !a)
- GF(q1->q0) definitely holds since we we never have q1, so q1->q0 does always hold
- GF(q2->q1) does not hold, since we always have q2 but never q1.
A path can only be accepted if all conditions would hold, but that is not the case for the only path that exists in the automaton. Hence, the automaton does not accept any word, and therefore the LTL formula is valid.