Your question does not make sense. {c,d} is a set of variables, and we can only compute ROBDDs for propositional formulas. The task is to compute the existential quantification over the variables c,d on the formula ¬ϕ. With the variable ordering given, this is straightforward, since the variables c,d appear topmost. Thus, we just have to compute the BDD for ¬ϕ and then make a cut between variables {c,d} and {a,b} which gives us some (at most four) BDDs on variables {a,b}. We then have to compute the disjunction of these BDDs.
The BDD is as follows:
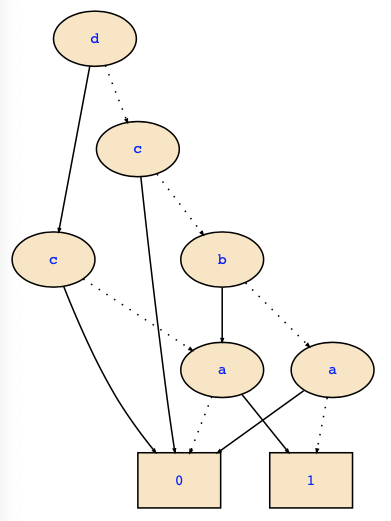
The cut mentioned above yields the three formulas false, a, a<->b so that the result would be the disjunction of these formulas. The Shannon normal form would then by (b?a:1).