You need to understand the meaning of sequents: The semantics of a sequent {g1,...,gm} |- {d1,...,dn} is the semantics of the formula g1 & ... & gm -> d1 | ... | dn. Recall also the special cases of an empty conjunction, which is true and an empty disjunction which is false. Hence, {} |- {d1,...,dn} means true -> d1 | ... | dn, i.e., d1 | ... | dn, and {g1,...,gm} |- {} means g1 & ... & gm -> false, i.e., !(g1 & ... & gm).
The rules of the sequent calculus just perform equivalent transformations such that the root sequent of a proof tree is equivalent to the conjunction of the leaf sequents.
So, if you construct a proof tree for {} |- {(c->b)->a}, you are transforming the formula (c->b)->a itself, and when you get the leaf sequents {}|-{a,c} and {b}|-{a} it means that (c->b)->a is equivalent to (a|c) & (!b|a).
If you construct a proof tree for {(c->b)->a} |- {}, you are transforming the formula !((c->b)->a), and when you get the leaf sequents {c}|-{b} and {a}|-{} it means that !((c->b)->a) is equivalent to (!c|b) & (!a).
The two proof trees are as follows (you mixed them up!):
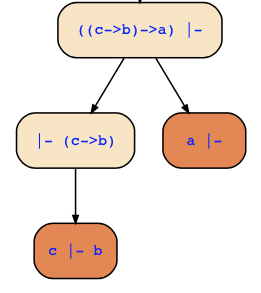
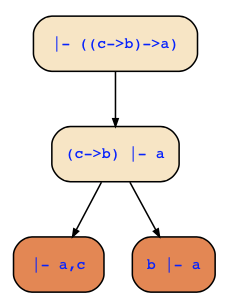
Moreover, a root sequent is valid if and only if all leaf sequents are valid. In other words, it is not valid if one of its leaf sequents is not valid, and the counterexample of that leaf sequent is then also a counterexample to the root sequent.