I guess that you have a typo in your formulas; and I guess you mean
A∃({p}, ¬p, ¬p ∧ a ∨ p ∧ ¬a ∧ ¬p, G(¬p))
A∃({p}, ¬p, ¬p ∧ a ∨ p ∧ ¬a ∧ ¬p, G(p)
Both of these define the same state transition diagram, i.e., two states that have the following transitions:
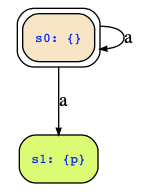
Okay, now to your question: Whether a state is safe or unsafe is determined by the acceptance condition of a safety automaton. For your first automaton, the acceptance condition is G(¬p) which declares all states that satisfy ¬p as safe states. That means only state s0 in the above figure, so we must not leave that state.
In the second automaton, the safe states are those satisfying p which is state s1 only. But since s0 is the initial state, there is no accepting path in that automaton, so it does not accept any word at all.
For liveness automata with acceptance condition F phi, there are no safe state, but states that are must be reached, and Büchi automata have fair states, i.e., a set of states that must be visited infinitely often.