State Transition Diagram (Exercise)

Question

In exercise 4, problem number 2a, I am facing the problem. Can anyone tell me what's wrong with my solution. The question is: Given a FSM: 

A={2Vin,2Vout,I,2Vstate,R}A={2Vin,2Vout,I,2Vstate,R}
where Vin={a}Vin={a}, Vout={o}Vout={o}, Vstate={p,q}Vstate={p,q}, I=I=q,
R=!(next(q)&p&q|next(p)|(o->a))

Answer 1

To see all transitions, you would have to compute a canonical DNF, i.e., fully expanded DNF, e.g., as follows extneding your computation to a DNF:

     ¬(next(q)∧p∧q ∨ next(p) ∨ (o->a))
     <-> ¬(next(q)∧p∧q  ∨  next(p)  ∨  (¬o ∨ a))
     <-> (¬next(q) ∨ ¬p ∨ ¬q)∧¬next(p)∧o∧¬a
     <-> ¬next(q)∧¬next(p)∧o∧¬a ∨ ¬p∧¬next(p)∧o∧¬a ∨ ¬q∧¬next(p)∧o∧¬a
     <-> ¬p∧¬q∧¬a∧o∧¬next(p)∧¬next(q) ∨ 
         ¬p∧¬q∧¬a∧o∧¬next(p)∧ next(q) ∨ 
         ¬p∧ q∧¬a∧o∧¬next(p)∧¬next(q) ∨ 
         ¬p∧ q∧¬a∧o∧¬next(p)∧ next(q) ∨
          p∧¬q∧¬a∧o∧¬next(p)∧ next(q) ∨ 
          p∧¬q∧¬a∧o∧¬next(p)∧¬next(q) ∨
          p∧ q∧¬a∧o∧¬next(p)∧¬next(q)  

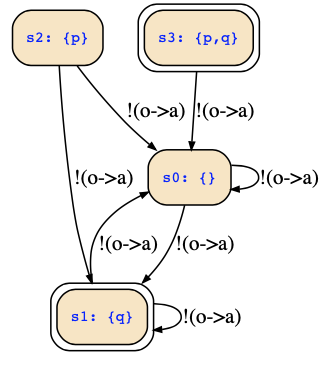
However, that is usually a lot of work and is not recommended. You can better compute the transitions as follows: With state variable p and q, we have states {},{p},{q},{p,q}. To compute their transitions, we instantiate the transition relation  with their possible values:

    {}    : ¬(next(p) ∨ (o->a))
    {p}   : ¬(next(p) ∨ (o->a))
    {q}   : ¬(next(p) ∨ (o->a))
    {p,q} : ¬(next(q) ∨ next(p) ∨ (o->a))

Now you see that states {},{p},{q} have the same transitions, namely two transitions both labeled with ¬(o->a) and leading to {} and {q}, respectively. This is so, since ¬(next(p) ∨ (o->a)) is equivalent to ¬next(p) ∧ ¬(o->a)).

The transitions of the remaining state {p,q} are given by ¬(next(q) ∨ next(p) ∨ (o->a)) which is equivalent to ¬next(q) ∧ ¬next(p) ∧ ¬(o->a), so that there is only one transition labeled with ¬(o->a) and leading to {}.

Hence, this is your FSM: