Finite Automata of LR(0) Items

Question

Hello,

I am a little confused about the construction of the automaton for LR(0) items.

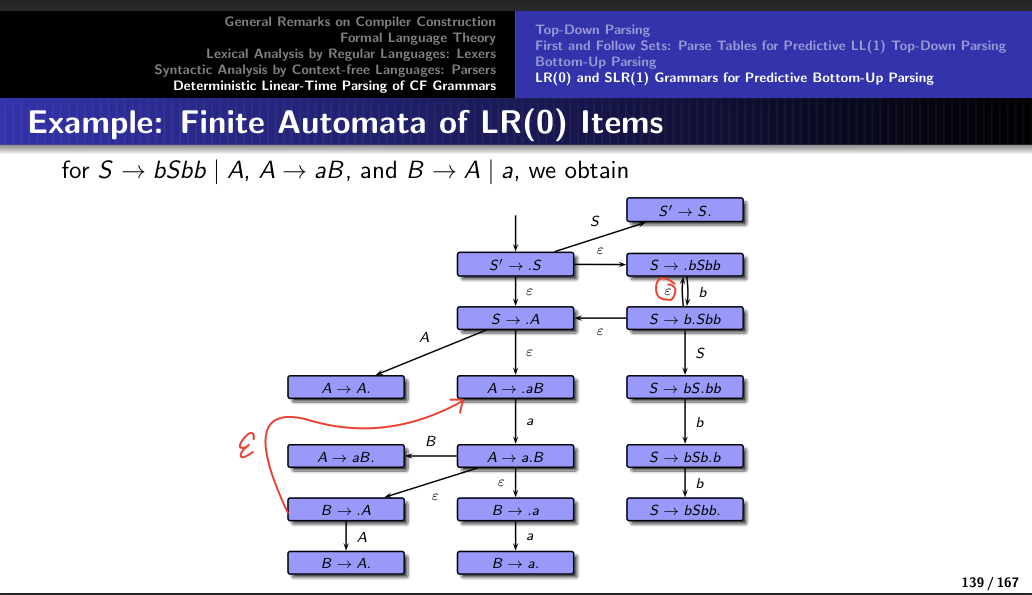
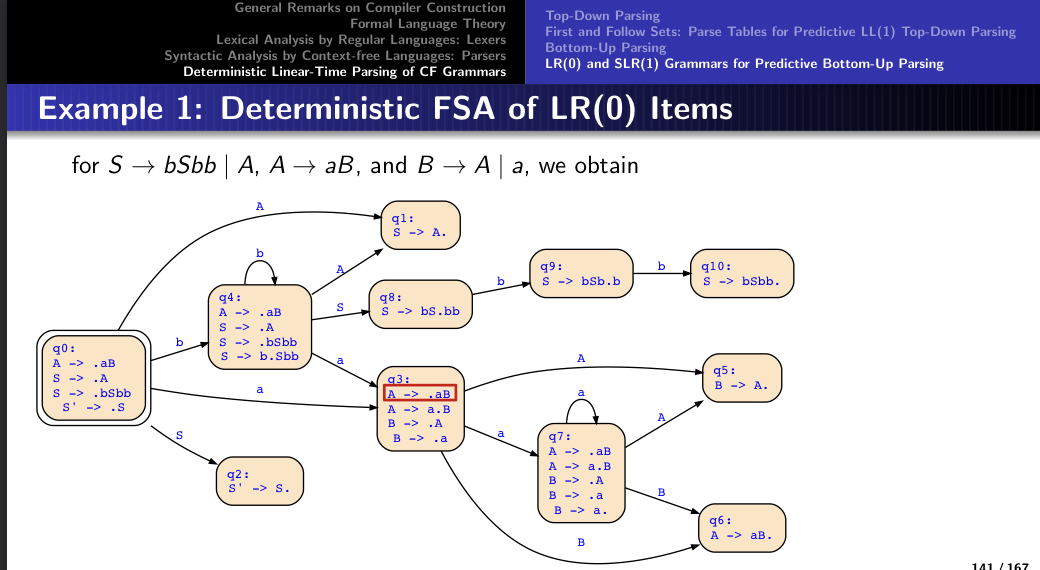
In case you don't see the picture, I am referring to slides 139 and 141 of the compiler frontend.

Slide 139: In the automaton given here, you can see an epsilon transition:

(S -> b.Sbb) -(e)-> (S -> .bSbb)

However, no epsilon transition is seen for the following state:

(B -> .A)

My question now is why there is no epsilon transition attached here.

Is it not possible that the following transition would be legitimate?:

(B -> .A) -(e)-> (A -> .aB)

If not, does a conflict occur here and why does it occur?

Furthermore, I can't explain the following state of the deterministic automaton (slide 141):

q0 -(a)-> q3

In the state q3 the rule A->.aB can be seen. The only way I can explain this state is:

(Starting at q0): (A -> .aB) -(a)-> (A -> a.B) -(e)-> (B -> .A) -(e)-> (A -> a.B)

Did I understand this wrong?

Best regards

Answer 1

You are right, there was a transition missing in the nondeterministic automaton of LR(0) items. Thank you for pointing this out; it has now been fixed in the slides and looks now as follows:

About your doubts on the transition q0 -(a)-> q3 of the deterministic automaton of LR(0) items: To generate q0, we start with the initial state "S'->.S" of the nondeterministic automaton and add all states that can be reached by epsilon-transitions which are "S->.A", "S->.bSbb", and "A->.aB". Now, your doubt is the transition for terminal symbol "a". To get those, we have to check all transitions of the states "S'->.S", "S->.A", "S->.bSbb", and "A->.aB" of the nondeterministic automaton for for terminal symbol "a": While "S'->.S", "S->.A", and "S->.bSbb" do not have such a transition, "A->.aB" has a transition to "A->a.B" which will create our successor state.

To complete the successor state, we have to add all states reachable by epsilon-transitions from "A->a.B" which are "B->.a", "B->.A", and "A->.aB" so that these states form our successor state q3 for the transition q0 -(a)-> q3 in the deterministic automaton.

Comments

Thank you very much! :)
The protocol (Fragestunde 22.03) says that no automata need to be constructed for context free grammars. That means that the automata shown above do not need to be constructed (but the parsing tables still do), right? I am asking, because in your Email about LR-Parsing (04.02) it is mentioned: „you should be able to determine its LR(0)-automaton“

---

No, that is a misunderstanding. The protocol means that it is not required to generate pushdown automata for *general* grammars. You can generate parsers as pushdown automata for any context-free grammar. However, for compilers, we are only interested in deterministic pushdown automata (and grammars), thus, you only need to be able to generate the top-down and bottom-up parsers for LL and LR grammars. To that end, you need to construct the deterministic LR(0) automaton either by determinization of the nondeterministic one or in a direct manner. You may have a look at the updated lecture slides that contains some notes about the construction of pushdown automata for general grammars (even though that has been excluded from the exam).