RoSy - Action Table

Question

Hallo,

ich hätte folgende Fragen zu der Konstruktion von Action Tables für LR0 Grammatiken.

Ich möchte mich konkret auf Beispiel 1 im Skript (Seite 185) beziehen.

Wann schreibt man Reduce(x -> y) bei einem bestimmten Action und bei einem anderen nicht. (für den betroffenen Zustand)?

Also zum Beispiel q1 hat ja S -> A. mit Punkt am Ende, dass heißt algorithmisch gesehen, dass hier ein Reduce in der Tabelle geschrieben soll. Ok, warum aber es nur für Actions b und $ geschrieben wurde und nicht bei a auch?

Auch bei z.B q5, sollte man hier nicht Reduce (B -> A) schreiben für a,b,$? warum nur für b,$

Grüße.

Answer 1

Hallo,

ich denke, dass es um die LR-Parsetabelle für die folgende Grammatik geht:

    S -> A | bSbb
    A -> aB
    B -> A | a

Der LR-Automat dieser Grammatik sieht folgendermaßen aus:

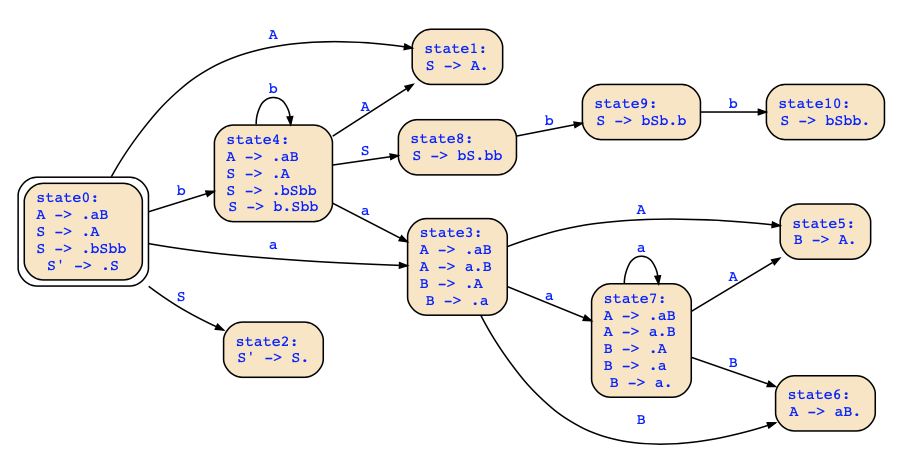
und die Parsetabelle, auf die sich die Fragen beziehen, sieht folgendermaßen aus:

Bei der LR(0)-Parsetabelle würde man die Aktionen folgendermaßen definieren [Seite 178]:

• wenn der Zustand q_i eine Regel A → α.aβ mit a ∈ T enthält, und q_i′ der Zustand ist, der im Automaten von q_i beim Lesen von a erreicht wird, dann schiebe a auf den Stack und lege q_i′ darüber
• wenn der Zustand q_i eine Regel S′ → S. enthält und die Eingabe ε ist, akzeptiere
• wenn der Zustand q_i eine Regel B → γ. enthält, dann reduziere mit Regel B → γ

Allerdings sehen wir, dass diese Regeln die Aktionen der LR(0)-Parsetabelle nicht eindeutig festlegen [Seite 179]. Zum Beispiel könnten wir in Zustand q₇ mit B → a reduzieren, da B → a. im Zustand enthalten ist und wir könnten andererseits in Zustand q₇ das Zeichen a schieben, da A → .aB in diesem Zustand enthalten ist. Diese Grammatik kann daher nicht mit einem LR(0)-Parser geparst werden (jedenfalls nicht ohne Backtracking oder nichtdeterministische Auswahl von Aktionen).

Allerdings geht man beim LR-Parsing in der Regel von SLR(1)-Parsetabellen (und in der Praxis sogar noch von LALR(1)-Parsetabellen) aus. Wenn wir in RoSy von LR-Parsern sprechen, meinen wir in der Regel SLR(1)-Parser, da deren Erweiterung gegenüber LR(0)-Parsern sehr einfach ist [Seite 81]: Bei SLR(1)-Parsetabellen wird eine Reduktion B → γ. nur erlaubt, wenn B → γ. dem Zustand angehört und das nächste Zeichen im Wort zu FOLLOW(B) gehört.

Also brauchen wir für unsere Grammatik zunächst die FOLLOW-Mengen:

    Follow(A) = {$,b}
    Follow(B) = {$,b}
    Follow(S) = {$,b}    

So, nun wirklich zu den Fragen: q₁ enthält S -> A., kann aber eine Reduktion nur machen, wenn das nächste Zeichen im Wort in Follow(S) = {$,b} liegt. Analog enhält q₅ die Aktion B -> A., kann bei SLR(1) aber nur mit dieser Regel reduzieren, wenn das nächste Zeichen im Wort in Follow(B) = {$,b} liegt. Daher scheiden dies Reduktionen aus, wenn das nächste Zeichen im Wort der Buchstabe "a" ist.

Somit bekommen wir die obige SLR(1)-Parsetabelle, welche in jeder Situation nicht mehr als eine Aktion bestimmt und damit einen deterministischen Kellerautomaten beschreibt.