You need to distinguish between syntax and semantics. From the syntax (as given by the above grammar rules), it is quite straightforward to decide whether a CTL* formulas belongs to LTL: It just has to start with A, and then no further path quantifier A or E is allowed afterwards.
For the semantics, the problem is much more difficult: Here, the question is whether the given CTL* formula can be rewritten to an equivalent one in LTL syntax. Here, you have to use some experience, and also need to understand the formula. Also, the following theorem may be of great help:
Theorem ([3]): Given a CTL formula φ, let ψ be the quantifier-free formula that is obtained by removing all path quantifiers from φ. Then, there is an equivalent LTL formula for φ iff Aψ is equivalent to φ.
Considering the formula ¬EF(¬E([1 U a] ∧ Fa)), we first have to drive the negation inwards and get first AG¬¬E([1 U a] ∧ Fa), and then AG E([1 U a] ∧ Fa). Next, I assume the U is a strong Until, and if so, then [1 U a] is equivalent to Fa, so that we have AG E(Fa ∧ Fa), i.e., AG EFa. That is not a LTL formula, but it is a CTL formula. According to the above theorem, it would only be equivalent to a LTL formula iff it would be equivalent to AGFa, but that is not the case.
You can use the following counterexample to distinguish between AG EF a and AGFa:
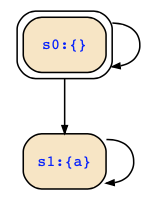
Using CTL model checking, you can quickly check that EF a holds on {s0,s1} and therefore also AG EF a holds on the same states. However, AGFa means that on all outgoing paths, a should hold infinitely often which is not the case in state s0, since there we can loop in s0.
Hence, AG EFa and AGFa are not equivalent, and hence, there is no LTL formula equivalent to the CTL formula AG EF a.