Exam Paper: 2020.08.25 : 8a

Question

In the below questions- 

Solutions:

a. AG((Fa) ∧ (Fb) ∧ (Fc))

AGA((Fa) & (Fb) & (Fc))

AGAFa & AGAFb & AGAFc

AGAF(a &b&c)

b. EGE((Fb) ∧ (Fa))

EGEF(b&a)

Are these incorrect?

Answer 1

The following formulas are equivalent to each other:

• AG((Fa) ∧ (Fb) ∧ (Fc))
• AGA((Fa) & (Fb) & (Fc))
• AGAFa & AGAFb & AGAFc

However, only the last one is a CTL formula (as required by the exercise).

Moreover, the fourth version mentioned, i.e, AGAF(a&b&c) is not equivalent to the three formulas above. It is equivalent to AGF(a&b&c) and means that on all paths we must have infinitely many points of time where we have a&b&c, while the other version just means that on all paths, we must have infinitely many a,b,c but these may not necessarily occur together (see also the counterexample below).

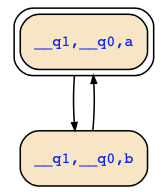
Second, the formulas EGE((Fb) ∧ (Fa)) and EGEF(b&a) are not equivalent for a similar reason: The second formula demands that there there are always points of time where a&b occurs together while the former only demands that a and b occurs. Check the following counterexample where we have E((Fb) ∧ (Fa)) in both states, thus EGE((Fb) ∧ (Fa)), but no state satisfies EF(b&a).

Answer 2

a. Your solution is slightly more strict than the original formula. The original formula wants a, b, and c to occur infinitely often on every path. Your formula wants infinitely many states that satisfy a&b&c at the same time. A loop going through {a}, then {b}, then {c}, then back to {a} would satisfy the first formula but not yours.

b. Similar bug. Your formula is looking for a&b in the same state. The original formula is fine if both a and b occur in any order (as long as both of them occur infinitely often on the same path).