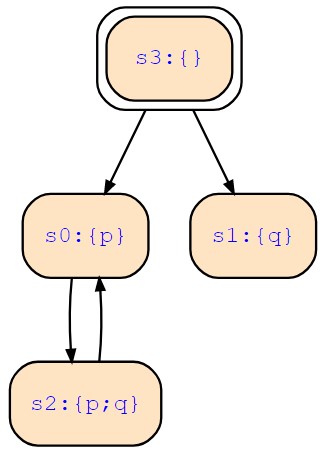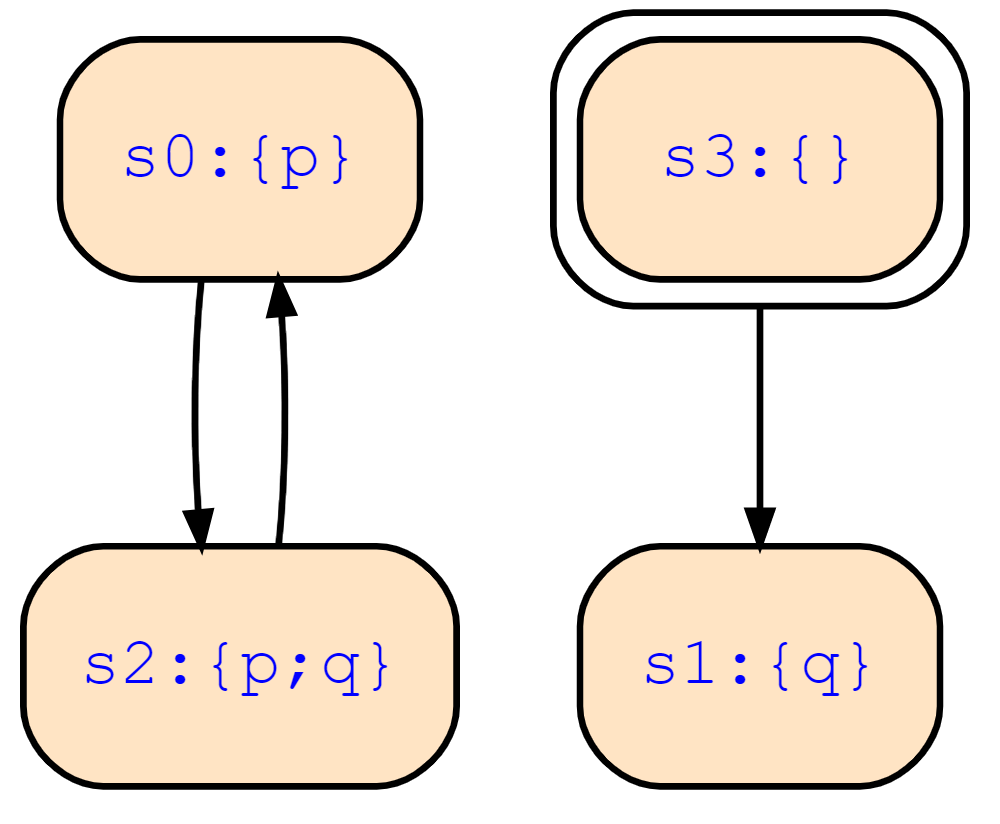
We want to prove whether AGp holds by means of induction. Check whether the property p is inductive (i.e. whether p -> [ ] p holds).
Property p should be inductive on this structure because the states {p} and {p,q} are universal predecessors of p.
However, I'm not sure whether the induction base is valid because the initial state does satisfy p -> [ ] p in the sense that we're in !p. Due to the missing transition from the initial state to the p-states however, the states satisfying p -> [ ] p cannot be reached which is why I'm not sure whether the induction base is valid.
If there needs to be a transition, the induction base should be satisfied by this structure, right?