2020 February Exam paper CTL, LTL and CTL*

Question

Question 7. a) What would a path satisfying S2 = XXG((a ⊕ Xa) ∧ (b ⊕ XXb)) look like?

(Not from the Exam paper). What is a & Fa? Is the answer a or Fa?

Answer 1

(a & F a) is equivalent to  a since a implies F a.

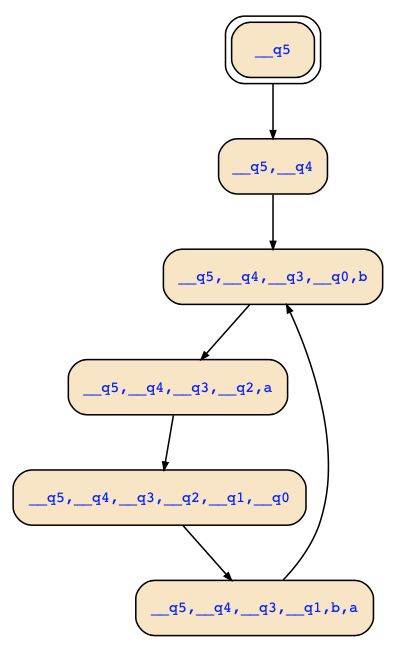
Here is a path made by the teaching tool satisfying S2 = XXG((a ⊕ Xa) ∧ (b ⊕ XXb)) where

    q0 = X a
    q1 = X b
    q2 = X X b
    q3 = G((a ⊕ Xa) ∧ (b ⊕ XXb))
    q4 = X G((a ⊕ Xa) ∧ (b ⊕ XXb))
    q5 = X X G((a ⊕ Xa) ∧ (b ⊕ XXb))

Answer 2

1. There are multiple paths. Let's just look at G((a ⊕ Xa) ∧ (b ⊕ XXb)) (the XX before it just means that the formula is evaluated from the third step on): The first part in the conjunct that has to hold globally, is (a ⊕ Xa). It just means that a is alternating every step, like a, ¬a, …. (b ⊕ XXb) means that b alternates compared to the next-next step, like b, ¬b, ¬b, b, or b, b, ¬b, ¬b, …. Together, that's a cycle among these four states: {}, {a}, {b}, {a,b}. (Either in this order or backwards)
2. a → F a (in words: When you satisfy a in the first step, then you have already satisfied a after finitely many steps). Thus, in the conjunction F a is redundant. As it is a conjunction, any satisfying assignment needs to satisfy both a and F a. Due to the implication, an assignment that satisfies a also satisfies F a. Hence, a ∧ F a = a.