I can read the following formula from the diagram:
d&c&!b&!a | d&!c&b&!a | !d&c&b&!a | !d&c&!b | !d&!c
Let's first make a Shannon decomposition to make the problem smaller:
d => c&!b&!a | !c&b&!a
| c&b&!a | c&!b | !cand yet another one on c:
d => c => !b&!a
| b&!a
| c => b&!a | !b
| 1
The ZDD for !b&!a is just the 1-leaf which is seen as follows: A full expansion will be the decision diagram (b=>(a=>0|0)|(a=>0|1)); you may wish to draw that here. Here, we apply the elimination rule to both nodes (a=>0|0) and (a=>0|1) since their high-part is 0; what is left is their low part, i.e., we have (b=>0|1). Again, we apply the elimination rule since the high-part is 0, and what is left is the low part, i.e., 1.
Next, construct the ZDD for b&!a. The full expansion will be the decision diagram (b=>(a=>0|1)|(a=>0|0)) which is reduced to (b=>1|0).
The ZDD for b&!a | !b is found by the reducing the full expansion (b=>(a=>0|1)|(a=>1|1)) which reduces to (b=>1|(a=>1|1)).
Finally, we need to determine the ZDD for 1 on variables b,a. Again, we consider the full expansion (b=>(a=>1|1)|(a=>1|1)) and see that we cannot eliminate any node.
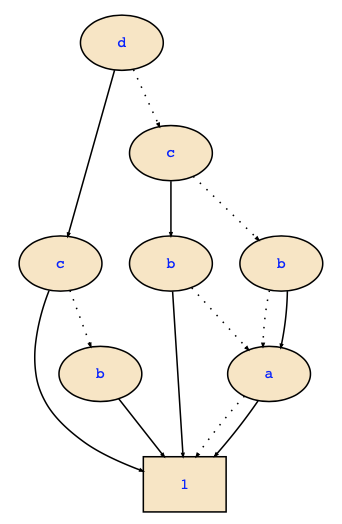
Hence, we now obtain
d => c => 1
| (b=>1|0)
| c => (b=>1|(a=>1|1))
| (b=>(a=>1|1)|(a=>1|1))This corresponds with the following ZDD: