Well, either you make case distinctions on the variables in the given orders (top-down approach), or you compute the BDDs using the Apply algorithm bottom up. The first approach is typically simpler for such examples (even though the Apply algorithm is more efficient in terms of algorithms). For the above example, you should obtain the following two BDDs:
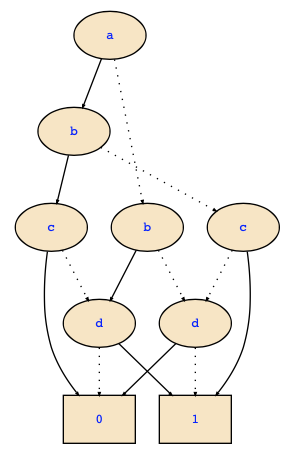
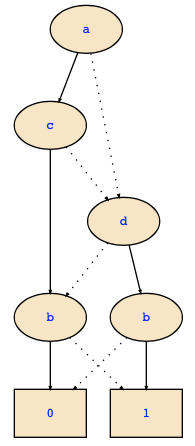
For example, the second BDD can be computed as follows using the top-down approach:
¬(d → (a ∧ c)) ↔ b
= (a => ¬(d → (1 ∧ c)) ↔ b | ¬(d → (0 ∧ c)) ↔ b)
= (a => ¬(d → c) ↔ b | d ↔ b)
= (a => (c => ¬(d → 1) ↔ b | ¬(d → 0) ↔ b) | (d↔b))
= (a => (c => ¬b | (d↔b)) | (d↔b))
Now,
d↔b
= (d => b | ¬b)
= (d => (b=>1|0) | (b=>0|1))
and hence
¬(d → (a ∧ c)) ↔ b
= (a => (c => ¬b | (d↔b)) | (d↔b))
= (a => (c => (b=>0|1) | (d => (b=>1|0) | (b=>0|1))) | (d => (b=>1|0) | (b=>0|1)))The formula is satisfiable since the BDDs have a path to the 1-leaf (all such paths are satisfying assignments).