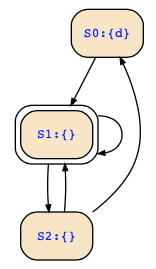
The computation given on the slides is correct. The Kripke structure we discuss here is the following one:
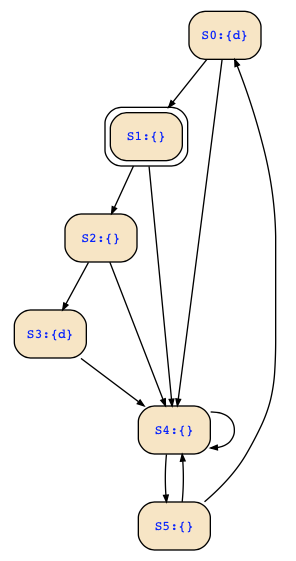
For the given Kripke structure, you start with the following relation which relates all pairs of states with each other that have the same label:
B0 = {(S0,S0);(S1,S1);(S2,S2);(S3,S3);(S4,S4);(S5,S5);
(S0,S3);(S1,S2);(S1,S4);(S1,S5);(S2,S4);(S2,S5);(S4,S5);
(S3,S0);(S2,S1);(S4,S1);(S5,S1);(S4,S2);(S5,S2);(S5,S4)}
Please consider the way I wrote it. There is always the part where each state is related with itself, and then rest consists of two halves which are symmetric to each other. The part where each state is related with itself does not need to be checked in the further steps, since these pairs will always remain in the relations. If you would check them, you would always find corresponding transitions since the upper and lower part are the same, and each pair (Si,Si) remains in the relation.
For the other pairs, we can say that if one is removed, then also its symmetric partner can be removed at the same time without further checking.
We may also list the currently bisimilar states of relation B0 for each state
---------------------
S0 S1 S2 S3 S4 S5
---------------------
S0 X X
S1 X X X X
S2 X X X X
S3 X X
S4 X X X X
S5 X X X X
---------------------
Note that we only need to consider an upper triangle or lower triangle of that table due to the above remarks. Then, you have to check the simulation diagrams below:
S0 --> {S1;S4}
|
S3 --> {S4}
S1 --> {S2;S4}
|
S2 --> {S3;S4}
S1 --> {S2;S4}
|
S4 --> {S4;S5}
S1 --> {S2;S4}
|
S5 --> {S0;S4}
S2 --> {S3;S4}
|
S4 --> {S4;S5}
S2 --> {S3;S4}
|
S5 --> {S0;S4}
S4 --> {S4;S5}
|
S5 --> {S0;S4}
Checking them means that you have to check whether for all transitions on the upper part, there is a simular one on the lower part and vice versa (since we compute a bisimulation relation).
- We drop (S1,S2) since for S2 --> S3 we need to find a bisimilar transition in S1 --> {S2;S4}, but neither (S2,S3) nor (S4,S3) is in B0. We also drop (S2,S1).
- We drop (S1,S5) since for S5 --> S0 we need to find a bisimilar transition in S1 --> {S2;S4}, but neither (S0,S2) nor (S0,S4) is in B0. We also drop (S5,S1).
- We drop (S2,S4) since for S2 --> S3 we need to find a bisimilar transition in S4 --> {S4;S5}, but neither (S3,S4) nor (S3,S5) is in B0. We also drop (S4,S2).
- We drop (S4,S5) since for S5 --> S0 we need to find a bisimilar transition in S4 --> {S4;S5}, but neither (S0,S4) nor (S0,S5) is in B0. We also drop (S5,S4).
This way, we get
B1 = {(S0,S0);(S1,S1);(S2,S2);(S3,S3);(S4,S4);(S5,S5);
(S0,S3);(S1,S4);(S2,S5);
(S3,S0);(S4,S1);(S5,S2)}
which looks like
---------------------
S0 S1 S2 S3 S4 S5
---------------------
S0 X X
S1 X X
S2 X X
S3 X X
S4 X X
S5 X X
---------------------This means that states {S0,S3}, {S1,S4} and {S2,S5} are equivalence classes so that the quotient structure just needs these three states: