LTL Equivalence - Exercise sheet does not accept checked solution from tool

Question

Hello,

I struggle getting my solution accepted in the exercise sheet.

For

S1 = X c & F b

S2 = X c & G b

I verified that S1 -> S2 is not valid, hence I try to construct 2 formulas for satisfying S1 but not S2.

I got

phi1 = !b&!c & (G( (!b&!c <-> X b&c) & !a))

phi2 = !a&!b&!c & (G(!a&!b&!c <-> X (a&b&c)))

Thanks again for answering the other questions here in the forum, they helped me alot to answer the a) and b) part of the exercise. However in the c) part, the exercise sheet does not accept the phi1 and phi2 seen above, although I checked it with the LTL tool.

I am confident in these solutions, but maybe I am currently staying on the "Leitung" or the exercise sheet does not accept this solution although it is right (hopefully).

Answer 1

Hmh, I see what you have done and you will be annoyed when you will realize what is wrong: As you want to show that S1&!S2 is satisfiable, you tried a proof for S1->S2 and got the following counterexample for (X c & F b) -> (X c & G b):

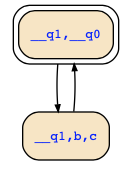
You described it with the formula 

        phi1 = !b&!c & G( (!b&!c <-> X b&c) & !a)

but it should be rather (I come back to this later):

        phi1 = !b&!c & G((!b&!c <-> X(b&c)) & !a)

To generate another formula phi2, you tried a proof of !phi1 & S1 -> S2, i.e., 

    !(!b&!c & G( (!b&!c <-> X b&c) & !a)) & (X c & F b) -> (X c & G b)

 which gave you

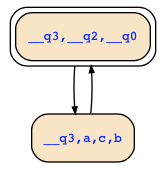
which you described as

        phi2 = !a&!b&!c & (G(!a&!b&!c <-> X (a&b&c)))

That far that good, now let's check what is wrong.

As already remarked above, you made a mistake in phi1 since you forgot brackets. Your formula phi1 is not satisfiable, since

    !b&!c & G( (!b&!c <-> X b&c) & !a)
    = !b&!c & G( (!b&!c <-> (X b) & c) & !a)
    = !b&!c & (G(!b&!c <-> (X b) & c)) & G(!a)
    = !b&!c & (G(c? (!X b) : b)) & G(!a)
    = !b&!c & (c? (!X b) : b) & X(G(c? (!X b) : b)) & G(!a)
    = !b&!c & b & X(G(c? (!X b) : b)) & G(!a)
    = false

You can check this also with the LTL prover by checking that the negation !phi1 of your formula phi1 is valid.

Since phi1 is false, the implications phi1 -> ... are trivially true, and the tool does not accept them (the exercise forbids to use a phi1 that is false because that would be as trivial as S1&!S2). 

Comments

Ohhhhh, I can not believe this :D
But I am happy that I was actually and kind of right. Thank you very much for clarifying this.