Well, considering CTL operators as abbreviations of µ-calculus formulas, I would first agree with saying νy.<:>(μx.(y∧b∨[]x)) and νy.<:>AF(y∧b) are the same. Also, it is clear that AFφ are the states where either all infinite paths finally reach φ-states (or where there are no outgoing paths at all).
But your main question is which states satisfy νy.<:>AF(y∧b) in general, i.e., not just on the structure shown in the exam. Such questions are hard to answer in general. Clearly, all well-formed formulas in µ-calculus have a meaning in the sense that there is in every transition system a corresponding set of states. But to describe those sets of states with a property that is meaningful for humans is not always simple. There are soo many µ-calculus formulas that you will soon have no intuition anymore on what they might want to tell you.
Still, let's have a little closer look on the formula that bothers you. For any transition system, its fixpoint iteration will start as follows:
- y[0] := S
- y[1] := [|<:>AF(y[0]∧b)|] = [|<:>AF(b)|]
- y[2] := [|<:>AF(y[1]∧b)|] = [|<:>AF((<:>AF(b))∧b)|]
So, we should understand which states satisfy <:>AFφ in general since we compute the fixpoint of the function f(y) := [|<:>AF(y∧b)|] . By the semantics, those states s must have a predecessor state s1 which satisfies AFφ (see the figure below):
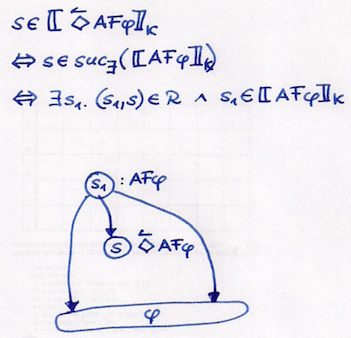
Now what are finally the states νy.<:>AF(y∧b) ? These belong to the set of states y where the above figure applies infinitely often, i.e.,
- those states that have a predessor state that satisfies AF(y∧b) and when you ask what y is inside this AF(y∧b), the answer is
- those states that have a predessor state that satisfies AF(y∧b) and when you ask what y is inside this AF(y∧b), the answer is ...
So, the English sentences 1 and 2 read in a loop are the answer to your question, even though I doubt that is one that is a satisfying one. We could research more on this miraculous set of states, and I guess that we will find out that all there infinite paths will infinitely often visit b-states which comes very close to the more satisfying answer you want to hear, I guess.
But as Martin wrote, these questions have in general no simple answer in human languages.