We first need to clarify what you want to describe. Should it be a Kripke Structure or an automaton? States of Kripke structures have labels, but their transitions don't; and Kripke structures have no accepting states. Automata have inputs and outputs which are the labels of their transitions, but their states don't have labels. Accepting automata do not have outputs.
What you described above is a kind a mixture of both. You have labels, but neither inputs nor outputs and your transitions have labels. Also, you have two sections of labels that both describe states starting with index 0.
Looking at the exercise, I can see that your task is to determinize a co-Büchi automaton. Let's consider as an example the one from the lecture notes. The following text describes that automaton:
inputs a0,a1;
init 0,2;
transitions
(0,a1,3); (3,a1,2); (2,a1,1);(1,a1,0);
(0,a0,0); (1,a0,1); (2,a0,2);(3,a0,3);
accept 2,3;where a1 means that we have input a and where a0 means that we have input !a (note that the above text is an explicit description of the automaton where we do not use propositional logic). The state transition diagram looks as follows:
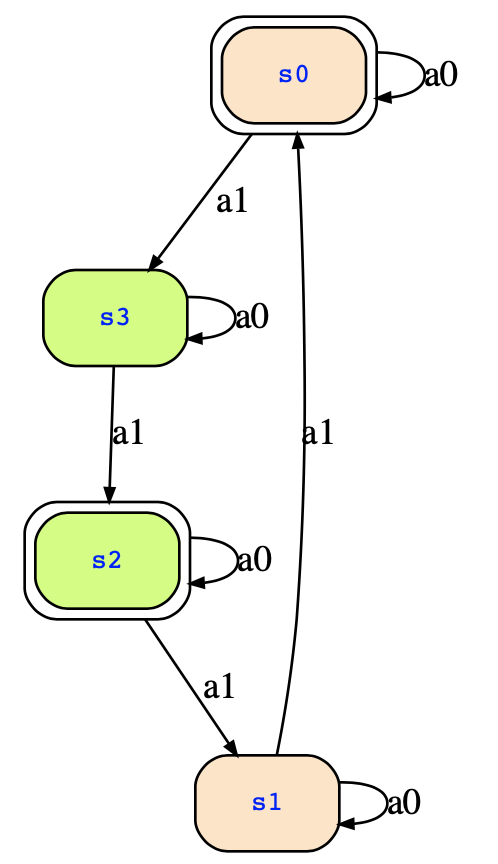
Determinizing this automaton with the breakpoint construction, you will obtain the following automaton:
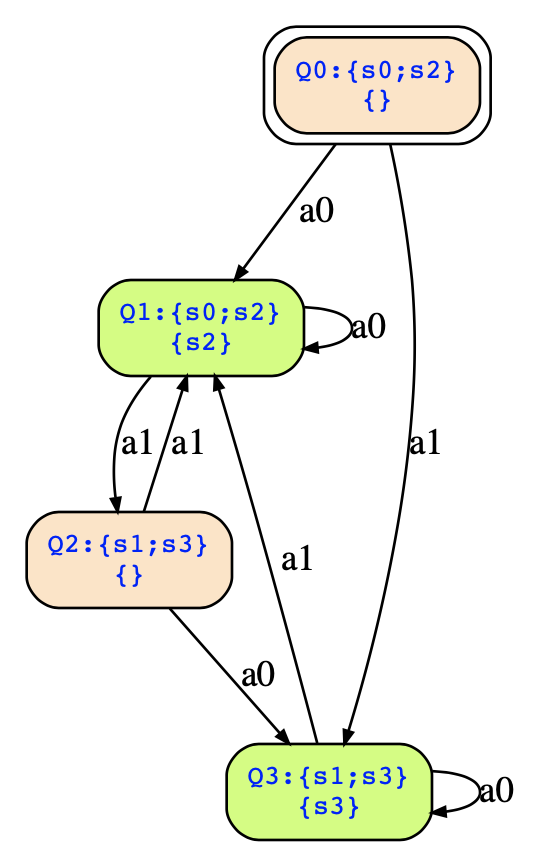
If you need to describe this one in text format, it should be done as follows:
inputs a0,a1;
init 0;
transitions
(0,a0,1); (0,a1,3);
(1,a0,1); (1,a1,2);
(2,a0,3); (2,a1,1);
(3,a0,3); (3,a1,1);
accept 1,3;Note that it is still an automaton in explicit form, and not a Kripke structure. It is not required to order the transitions in any way, but I recommend for deterministic automata to write per state one line and list the transitions for that state in that line. This way you can double check quickly that you described it complete and correct.