It is indeed a tautology which you can prove in various ways. Thanx for this question, and take the time to go through the answer below. Note that the question is essentially a question about the LTL formula [b WW b] and we may ask whether that one only on all paths. We can prove that in various ways:
First Way: Reduction to the Emptiness Problem of an Equivalent Omega-Automaton. We translate the negation of the formula to an equivalent existential omega-automaton and check that it cannot accept any word (if it would, that word would be a counterexample to our formula). For ![b WW b], we obtain the following omega-automaton using a single state variable q:
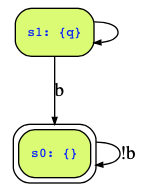
Auto∃({q},!q,q<->b|!b&next(q),F(!b->q))The state transition diagram of this automaton looks as follows:
and its associated Kripke structure looks as follows:
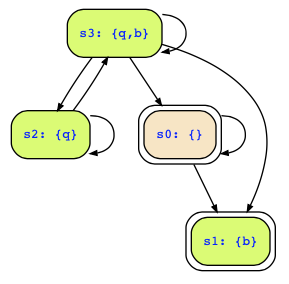
Now, we need to check whether there is an infinite path from an initial state that will at least once reach a state where !b->q holds, i.e., one of the green states. You can clearly see that the initial state s1 is a deadend state, so we can omitt it (since it has no infinite outgoing paths); but then only s0 remains as the only reachable state, and the only path is the one where we always stay in s0. That path, however, does not satisfy the acceptance condition, since we never enter a green state. Therefore, the automaton does not accept any word. Hence, there is no path that would satisfy ![b WW b], and conversely, all paths satisfy [b WW b].
Second Way: Use the given semantics. We prove that on all paths pi, we have pi,0 |= [b WW b]. According to the semantics, pi,0 |= [a WW b] holds iff there is a point of time t, where pi,t |= b holds, then we must also have pi,t |= a for the first one of these points of time t. In particular, we have pi,0 |= [b WW b] holds iff there is a first point of time t, where pi,t |= b holds, then we must also have pi,t |= b. But that is clearly the case, so that pi,0 |= [b WW b] holds on every path, and therefore A[b WW b] holds on every state of every Kripke structure.
Third Way: Proof Calculi. This is what you are maybe really interested in. For temporal logics, there are also proof calculi. In VRS, we do not consider them, since we are mostly interested in the verification of reactive systems which means checking whether a temporal logic property holds on a Kripke structure. These proof calculi are formulated in various ways like natural deduction, but also in tabuleaux form. Amir Pnueli has written papers about that, but also many others. At the end, the tableaux will also produce a Kripke structure which is nothing else than the associated Kripke Structure of the above omega-automaton, and we have to check the eventual properties in that structure similar to the emptiness check we discussed above. So, the proof calculi finally lead to nothing else than the first approach above which is the simplest one that can also be easily implemented.
Bytheway, some guys have embedded temporal logic in theorem provers so that one can use the proof rules of those theorem provers to prove temporal logic formulas (see https://es.cs.uni-kl.de/publications/datarsg/ScHo99.pdf). However, people were more enthusiastic about the automated proof procedure that came with the embedding that I implemented through the translation to omega-automata.